Volúmenes de sólidos
Se denomina solido de revolución o volumen de revolución, si una región en el plano es girada alrededor de una linea, el solido que resulta se llama solido de revolución y la linea es llamada el eje de revolución.
En las figuras anteriores los dos sólidos resultan de la revolución de una figura geométrica y una región parabólica alrededor de una recta . Se puede encontrar el volumen de los sólidos de revolución por dos métodos :
- Discos o Arandelas
- Cascarones cilíndricos
- Discos o Arandelas
- Cascarones cilíndricos
Método del disco o arandelas :
Si giramos una región del plano alrededor de un eje obtenemos un sólido de revolución. El volumen de este disco de radio R y de anchura ω es: -
Volumen del disco = π R^2 W
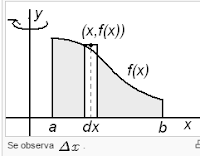
Para ver cómo usar el volumen del disco y para calcular el volumen de un sólido de revolución general, se hacen n particiones en la gráfica.
Para ver cómo usar el volumen del disco y para calcular el volumen de un sólido de revolución general, se hacen n particiones en la gráfica.
Estas divisiones determinan en el sólido n discos cuya suma se aproxima al volumen del mismo. Teniendo en cuenta que el volumen de un disco es , la suma de Riemann asociada a la partición, y que da un volumen aproximado del sólido es:
Por tanto, recordando la definición de integral definida de Riemann se obtiene que:
si se toma el eje de revolución verticalmente, se obtiene una fórmula similar :

- EJEMPLO :
Encuentre el volumen de la región limitada f(x)= x2+1,
alrededor de la recta x=3
Este vídeo les puede ayudar a entender mejor el análisis de arandelas o discos
Cascarones cilíndricos
Un cascaron cilíndrico es un solido acotado por dos cilindros circulares rectos como se en el bosquejo. El cilindro esta definido por el radio interno , el radio externo y por la altura.
El método de los
casquetes cilíndricos funciona muy bien en esta situación. Básicamente consiste
en dividir el sólido de revolución en una serie de casquetes cilíndricos que se
incrustan unos dentro de otros y en integrar luego los volúmenes de estos
casquetes para obtener el volumen total. En la se puede ver cómo
se van agregando y se van retirando sucesivamente estos elementos y cómo se
produce el sólido de revolución. Es por esto por lo que a este método se le
conoce también como el método de las "capas", las
"envolturas", las "envolventes" o los
"cascarones" cilíndricos.
Pero antes de
entrar en detalles es importante entender bien la estructura geométrica que
está involucrada en este método. Quizás resulte útil pensar en objetos
cotidianos que presentan la misma configuración.. El primero que viene a la
mente es posiblemente un trozo de cebolla pues es bien conocido el hecho de que
en su interior los tejidos de un trozo de este vegetal están dispuestos en una
serie de capas más o menos cilíndricas que, cuando se cortan transversalmente y
se sirven en las ensaladas, forman los característicos "anillos" de
la cebolla.
La aproximación del volumen sera mejor cuanto mas grande sea n, el numero de casquetes
cilíndricos encajados. Luego tenemos el siguiente volumen:

Es esta la formula general para el calculo de volúmenes con el método de los casquetes cilíndricos.
Resumamos:
El volumen del solido de revolución que se genera al hacer girar al rededor del y la región comprendida entre la curva y= f(x), con f(x) > 0, el eje x y las rectas verticales x=a y x=b, donde 0 <a <b , esta dado por la siguiente integral:

Este vídeo les puede ayudar a entender mejor el análisis de cascarones cilíndricos